- 01m18s
6 min de lecture
Brevet 2025 : découvrez le sujet et le corrigé de l'épreuve de mathématiques
Après le français, les candidats du diplôme national du brevet 2025 ont planché sur l'épreuve de mathématiques ce jeudi 26 juin. En partenariat avec digiSchool, RTL vous dévoile le sujet et le corrigé de l'épreuve.

Brevet 2025 : découvrez le sujet et le corrigé de mathématiques
Crédit : FREDERICK FLORIN / AFP
Je m'abonne à la newsletter « Infos »
Place aux mathématiques. Après le français ce jeudi matin 26 juin, les candidats du diplôme national du brevet (DNB) ont planché pendant deux heures l'après-midi sur le sujet de mathématiques. Les épreuves écrites du DNB se termineront ce vendredi 27 juin par l'histoire-géographie le matin et les sciences l'après-midi. Ce sera ensuite l'heure de la présentation orale de 15 minutes.
Les épreuves écrites du brevet des collèges sont notées sur 400 points : 100 points pour le français, 100 points pour les mathématiques, 50 points pour l'histoire-géo et l'EMC et 50 points pour les sciences.
L'épreuve de mathématiques se compose de plusieurs exercices qui mobilisent souvent une multitude de notions du programme. Retrouvez les sujets et le corrigé complet de l'épreuve en partenariat avec digiSchool.
Le sujet de l'épreuve de mathématiques
Voici le détail de la répartition des points, par exercice :
Exercice 1 :
On dispose d’une urne A contenant 6 boules numérotées : 7 ; 10 ; 12 ; 15 ; 24 ; 30
et d’une urne B contenant 9 boules numérotées : 2 ; 5 ; 6 ; 8 ; 17 ; 18 ; 21 ; 22 ; 25.
Les boules sont indiscernables au toucher.
1. On tire une boule dans l’urne A, quelle est la probabilité d’obtenir un nombre pair ?
2. On tire une boule dans l’urne B, justifier que la probabilité d’obtenir un nombre premier est de 1/3.
3. Quelle urne contient le plus grand nombre de boules dont le numéro est un multiple de 6 ?
4. On tire une boule au hasard dans l’une des urnes. Démontrer que la probabilité d’obtenir un nombre supérieur ou égal à 20 est la même quelle que soit l’urne choisie ?
5. En repartant avec la composition initiale des urnes A et B on décide d’ajouter une boule numérotée 50 dans chacune d’entre elles. Dans ces conditions, la probabilité d’obtenir un résultat supérieur ou égal à 20 est-elle toujours égale quelle que soit l’urne choisie ?
Exercice 2 :
Cette année, les professeurs d’EPS proposent aux élèves un aquathlon (course à pied et natation).
Partie A : la course à pied
Le parcours de la course à pied est représenté par le dessin ci-dessous (le dessin n’est pas à l’échelle) :
Le parcours est représenté par ACDEB avec le départ au point A et l’arrivée au point B.
Les points A, C, B sont alignés.
Les points A, D, E sont alignés.
ADC est un triangle rectangle en A.
AC = 480 m CB = 120 m
AE = 250 m DE = 50 m
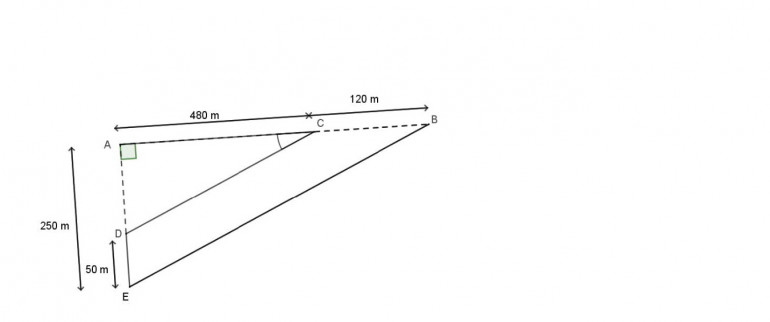
Dessin de la partie A de l'exercice 2 du brevet de maths 2025.
Crédit : Ministère de l'Éducation nationale
1. Justifier que AD = 200 m.
2. Calculer la longueur CD.
3. Pour que le parcours soit validé il est nécessaire que les droites (CD) et (BE) soient parallèles et que la mesure de l’angle 𝐴𝐶𝐷̂ soit supérieure à 20°.
a. Les droites (CD) et (BE) sont-elles parallèles ?
b. La mesure de l’angle 𝐴𝐶𝐷̂ est-elle supérieure à 20° ?
c. Le parcours est-il validé ?
Partie B : La natation
Concernant l’épreuve de natation, il s’agit de nager une distance de 200 m.
Voici les temps de 9 élèves : 5 min 30 s ; 5 min 45 s ; 5 min 49 s ; 5 min 50 s ; 6 min ; 6 min 11 s ; 6 min 12 s ; 6 min 20 s ; 6 min 40 s.
4. Quel est le temps médian de cette série ?
5. Un poisson rouge nage à la vitesse de 5 km/h. Nage-t-il plus vite que l’élève le plus rapide ?
Exercice 3 :
Cet exercice est un QCM avec une seule réponse exacte parmi les 4 propositions proposées.
Exercice 4 :
Au club "Mathsetmagie", on s’amuse à créer des programmes de calcul plus ou moins magiques.
Partie A : le programme de Zoé
Voici le programme de Zoe :
Choisir un nombre
Soustraire 4
Multiplier par 2
Ajouter 8
1. Vérifier que si on choisit 10 comme nombre de départ, on obtient 20 avec ce programme.
2. Quel résultat obtient-t-on avec ce programme si on choisit −7 comme nombre de départ ?
3. Zoé prétend que son programme est « magique » car, quel que soit le nombre choisi, le résultat est toujours le double du nombre de départ. A-t-elle raison ?
Partie B : le programme de Fred
Fred décide de faire son programme de calcul sur Scratch :
4. Démontrer que si le nombre de départ est x, le résultat obtenu avec le programme de Fred est 20x + 50.
5. Quel nombre faut-il choisir au départ pour obtenir 75 avec le programme de Fred ?
6. Constatant que son programme n’a rien de magique, Fred souhaite le modifier afin que le résultat soit toujours 20 fois plus grand que le nombre de départ. Recopier et compléter sur la copie la sixième ligne du programme pour que ce soit le cas.
Exercice 5 :
Un garage propose 2 options au client :
- Option Achat : prix d’achat de la voiture 22 400 €. Assurance obligatoire 75 € par mois.
- Option Location : 425 € par mois, assurance comprise.
L’objectif de cet exercice est de comparer ces deux options.
Partie A
1. Montrer qu’avec l’option Achat la dépense à la fin de la première année est de 23 300 €.
2. Après 36 mois, calculer l’économie réalisée par le client s’il choisit l’option Location ?
3. Afin de comparer les dépenses correspondantes à ces options le client a réalisé le tableau suivant à l’aide d’un tableur :

Un tableur de la partie A de l'exercice du brevet de maths 2025.
Crédit : Ministère de l’Éducation nationale
Quelle formule doit être saisie dans la cellule B3 qui, étendue jusqu’à la cellule F3, permet de compléter le tableau ?
Partie B
On souhaite maintenant modéliser les deux options précédentes par des fonctions.
On note 𝑥 la durée écoulée en mois depuis la livraison de la voiture.
La fonction 𝑔, permettant de calculer la dépense correspondant à l’option Location, peut s’écrire sous la forme : 𝑔(𝑥)=425𝑥.
4. Déterminer l’expression de 𝑓(𝑥) permettant de calculer la dépense correspondant à l’option Achat.
5. Sur le graphique de la page 8, on a tracé les courbes représentatives 𝐶𝑓 et 𝐶𝑔 des fonctions 𝑓 et 𝑔.
Par lecture graphique, déterminer à partir de combien de mois, l’option Achat est la plus avantageuse.
Le corrigé de l'épreuve de mathématiques
Exercice 1 :
1. On tire une boule dans l’urne A, quelle est la probabilité d’obtenir un nombre pair ?
Nombres pairs dans A : 10, 12, 24, 30 → 4 sur 6
→ Probabilité = 4 sur 6 = 2 sur 3
2. On tire une boule dans l’urne B, justifier que la probabilité d’obtenir un nombre
premier est de 1 sur 3
Nombres premiers dans B : 2, 5, 17 → 3 sur 9
→ Probabilité = 3 sur 9 = 1 sur 3
3. Quelle urne contient le plus grand nombre de boules dont le numéro est un multiple
de 6 ?
Multiples de 6 :
A → 12, 24, 30 → 3 boules
B → 6, 18 → 2 boules
→ donc A contient plus de multiples de 6
4. On tire une boule au hasard dans l’une des urnes. Démontrer que la probabilité
d’obtenir un nombre supérieur ou égal à 20 est la même quelle que soit l’urne choisie
?
Nombres ≥ 20 :
A → 24, 30 → 2 sur 6 = 1 sur 3
B → 21, 22, 25 → 3 sur 9 = 1 sur 3
→ Probabilité égale dans les deux urnes
5. En repartant avec la composition initiale des urnes A et B on décide d’ajouter une
boule numérotée 50 dans chacune d’entre elles. Dans ces conditions, la probabilité
d’obtenir un résultat supérieur ou égal à 20 est-t-elle toujours égale quelle que soit
l’urne choisie ?
Après ajout d’une boule 50 dans chaque urne :
A contient 7 boules, dont 24, 30, 50 ≥ 20 → 3 sur 7
B contient 10 boules, dont 21, 22, 25, 50 ≥ 20 → 4 sur 10 = 2 sur 5
→ Les probabilités ne sont plus égales car l’ajout modifie différemment le numérateur et le
dénominateur dans chaque cas.
Exercice 2 :
1. Justifier que AD = 200 m.
𝐴𝐸 = 𝐴𝐷 + 𝐷𝐸 car les points A, D, E sont alignés.
→ 𝐴𝐷 = 𝐴𝐸 − 𝐷𝐸 = 250 − 50 = 200𝑚
2. Calculer la longueur CD.
Triangle ADC rectangle en A
→ d’après le théorème de Pythagore :
𝐶𝐷2 = 𝐴𝐶2 + 𝐴𝐷2 = 4802 + 2002 = 230400 + 40000 = 270400
𝐶𝐷 = √270400 = 520 m
3.a. (CD) et (BE) sont-elles parallèles ?
On compare les rapports 𝐴𝐷 sur 𝐴𝐸 et 𝐴𝐶 sur 𝐴𝐵 :
𝐴𝐷 sur 𝐴𝐸 = 200 sur 250 = 0,8
𝐴𝐶 sur 𝐴𝐵 = 480 sur 600 = 0,8
Les points A, D, E sont alignés ; A, C, B aussi.
→ D’après la réciproque du théorème de Thalès, les droites (CD) et (BE) sont parallèles
3.b. Angle 𝐴𝐶𝐷
Dans triangle ADC rectangle en A :
tan( 𝐴𝐶𝐷) = 𝐴𝐷 sur 𝐴𝐶 = 200 sur 480 = 5 sur 12
→ 𝐴𝐶𝐷 ≈ arctan( 5 sur 12) ≈ 22,6°
3.c. Conclusion :
→ Droites (CD) et (BE) sont parallèles
→ 𝐴𝐶𝐷 > 20°
→ Le parcours est validé
Retrouvez l’intégralité du sujet du brevet de maths et son corrigé sur digischool.fr .





